Цифровой сигнал и его характеристики

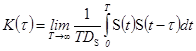, (3.13)

где T - длительность сигнала;

- дисперсия сигнала;

- временное расстояние между двумя сечениями сигнала.

При проведении расчетов АКФ воспользуемся возможностями программы Mathсad. Поступим следующим образом.

Создадим два вектора и (количество столбцов - 1, строк - число разрядов в 4-кодовых комбинациях):

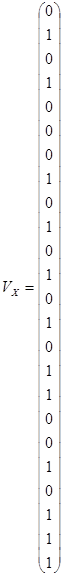
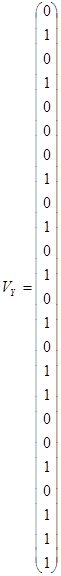
Далее воспользуемся функцией Mathсad .

В первом случае векторы одинаковы, и корреляция будет равна 1, т. е. .

Далее изменим вектор, сдвинув числа на один шаг, и вновь повторим вычисление корреляции. Это равносильно внесению временного сдвига на один шаг, т.е. на длительность одного импульса мкс. Таким образом рассчитывается АКФ.

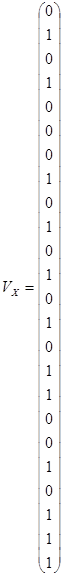
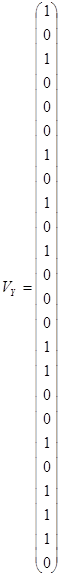
В этом случае .

Для выяснения статистических связей возьмем 8 значений векторов и corr.

Таблица 3.2 - АКФ кодового сигнала

В среде Mathсad по данным таблицы 3.2 сформируем два вектора - и :

.

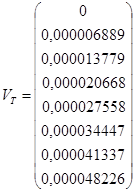
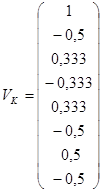На основании рассчитанной АКФ подберем математическое выражение, наиболее полно отражающее реальную зависимость. Для этого воспользуйтесь методом Mathсad, который называется «сплайн-аппроксимация». Исходная функция АКФ заменяется отрезками кубических полиномов, каждый из которых проходит через три смежные точки. Коэффициенты полиномов рассчитаны так, что первые и вторые производные непрерывны.

Операция сплайн-аппроксимации проводится в два этапа. На первом этапе с помощью одной из функций ( - для кубического полинома; - для квадратичного; - для линейного полинома) отыскивается вектор вторых производных заданной функции , которая в свою очередь должна быть задана векторами (абсциссы) и (ординаты). На втором этапе для каждой искомой точки вычисляется значение с помощью функции interp.

С помощью функции вычислим вектор VS вторых производных при приближении к кубическому полиному:

.

Далее вычисляем функцию, аппроксимирующую АКФ кубическим сплайн-полиномом:

.

Произведем кусочную аппроксимацию отрезками прямых

.

Обе рассчитанные зависимости приведены на рисунке 3.3. Сравнивая ход кривых, можно сделать вывод о степени приближения кубического сплайн-полинома и расчетных значений.

Интересное из раздела

Проектирование волоконно-оптических линий передач между городами Мелитополь-Луганск
Волоконно-оптические линии передачи (ВОЛП) на сегодняшнее время переживает расцвет, связанный, в первую очередь с взрывным характером развития в последние годы ...

20-разрядный аналого-цифровой преобразователь, изготовленный по технологии КМОП 0,9 пм
Традиционные конструкции аналого-цифровых преобразователей (АЦП) использовали параллельную архитектуру и биполярные технологии для получения 8-битного разрешени ...

Автоматизация судовой энергетической установки
Автоматическое управление технологическими процессами является одним из главных направлений научно-технического прогресса на морском транспорте. Автоматизация СЭУ обеспе ...