Исследование кода, позволяющего исправить двукратные ошибки

Построим график зависимости вероятности ошибки приема одиночного символа после декодера от отношения сигнал/шум на входе. График будет иметь вид, представленный на рис. 28.

Рис.2 8

ЗАКЛЮЧЕНИЕ

В ходе выполнения курсовой работы были получены следующие результаты:

1.Исследованы алгоритмы цифровой обработки сигналов в условиях как наличия и отсутствия помех. В ходе работы была спроектирована модель дискретной свертки в среде Mathcad 14.

.Исследованы кодопреобразователи циклических кодов и исследованы их корректирующие способности.

.Исследованы корректирующие способности кодов БЧХ. В ходе работы была спроектирована модель кода (15, 7) с проверкой на четность, исправляющего двукратные ошибки.

ПРИЛОЖЕНИЕ А. МОДЕЛЬ КОДА (15, 7) С ПРОВЕРКОЙ НА ЧЕТНОСТЬ, ИСПРАВЛЯЮЩЕГО ДВУКРАТНЫЕ ОШИБКИ

Для реализации этой модели необходимо ввести известные проверочные матрицы такого кода и вычислить все возможные синдромы с целью их дальнейшей сортировки в соответствии с позициями ошибок в кодограмме.

Для облегчения определения позиции ошибок в кодограмме расположим все возможные синдромы в виде треугольной матрицы на следующем screenshot.

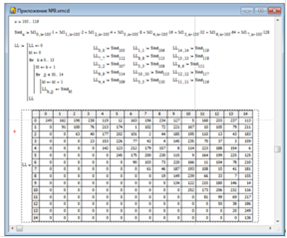
На примере определим позиции ошибок в кодограмме. Так если ошибки произошли на позициях 2 и 7, то результат вычисления синдрома соответствует SindD=l. В треугольной матрице этот синдром находится соответственно во 2-й строке 7-го столбца.

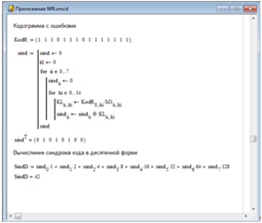
Для проведения исследования корректирующих способностей помехоустойчивого кода (15,7) необходимо многократно проводить подобные вычисления для различных значений мощности шума. Кроме того, для исправления ошибочной кодограммы необходимо определять программно позиции ошибок и формировать вектор ошибок. Данная операция представлена в части кода, приведенного ниже.

С целью более точного построения графиков помехоустойчивости необходимо произвести многократный расчет вероятностей ошибки Posh и Poh, а затем найти их среднее значение. Данную процедуру можно также осуществить в виде цикла подпрограммы.

ПРИЛОЖЕНИЕ Б. МОДЕЛЬ ДИСКРЕТНОЙ СВЕРТКИ СИГНАЛА

Из теории аналоговых фильтров известно, что сигнал Sv(t) на выходе фильтра выражается в виде свертки

где h(t) - импульсная характеристика фильтра (напоминаем - отклик фильтра на дельта-функцию ); S(t-τ) - входной сигнал.

Для реализации цифровых фильтров используется дискретная свертка

где h(kT) - дискретные значения (цифровые) импульсной характеристики фильтра; S[(n-k)T]- дискретные (цифровые) значения задержанного на k тактов входного сигнала.

Запишем период сигнала N. Далее запишем непосредственно сигнал Sln, фильтр hln и выражение для их свертки. Элемент кода представлен ниже.

Поскольку свертка двух функций осуществляется на двух периодах сигнала, то введено дополнительное обозначение сигнала и фильтра S2nnn и h2nnn, расширенных до длины nnn = 16, достаточной для визуального отображения. Обратите внимание на выражение, вычисляющее свертку Svnn, где индекс при S2 меняется в пределах от 1 до 7.

Для вычисления дискретной свертки сигнала на выходе фильтра можно использовать дискретное преобразование Фурье (ДПФ)

где Ω=2π/NT - основная частота преобразования, exp(-jΩT) = exp(-j2π/N) - отсчеты дискретной экспоненты, которая называется поворачивающим множителем, С(kΩ)=C(k) - коэффициенты ряда Фурье, число коэффициентов ряда равно числу отсчетов (N) дискретного сигнала.

Интересное из раздела

Проблемы обнаружения и подавления работы радиоуправляемых взрывных устройств
Цель контрольной работы - описать проблемы обнаружения и подавления работы радиоуправляемых взрывных устройств и сотовых телефонов, выявить основные методы ...

Анализ и синтез САУ методом корневого годографа
- Изучение системы автоматического регулирования (САР). - Оценка качеств, характеристик САР (устойчивости, ошибки, переходного процесса) по различн ...

Расчет линейной электрической цепи при гармоническом воздействии
Цель курсовой работы состоит в практическом освоении методов расчета простых и сложных электрических цепей при воздействии на них гармонических колебани ...