Избыточность и цифровая коррекция

Межкаскадная ошибка усиления в масштабе всего участка и смещение графика по вертикали вызывает ошибки в аналоговом входе следующего этапа, когда используется ненулевой остаток. Если ошибка в аналоговом входе следующего уровня для одного участка больше чем (где r - разрешение, остающееся после ошибки межкаскадного усиления), то ошибка преобразования не будет исправлена при цифровой коррекции. Для всех ненулевых остатков, затронутых ошибками межкаскадного усиления, границы преобразования не имеют какого-либо специального значения. Однако, эффект ошибки усиления является наибольшим для остатка с наибольшим значением, который такой же, как и в левом конце в идеальном случае. На практике нелинейность ADSC увеличивает остаток с одной стороны затронутых отсчетов, но величина остатка слева все равно больше любого другого значения, если нелинейность ADSC в пределах диапазона исправления. Поэтому эффект межкаскадной ошибки усиления при линейности ADSC ухудшается увеличенным остатком в левой части и в идеальном случае, и на практике. Кроме того, увеличенное значение остатка также увеличивает размах сигнала на выходе межкаскадного усиления.

Рисунок 4 - Идеальный остаток от входного сигнала с использованием компаратора

Для решения этих проблем, к схеме АЦП может быть добавлен компаратор чтобы уменьшить величину остатка в идеальном случае. На рис. 4 показан график получающийся при идеальном остатке для примера 2б. (Смещение компаратора здесь принимается равным нулю.) Порог дополнительного компаратора от - 3/4 Vr, и этот компаратор не изменяет выходной цифровой сигнал этого уровня, а только ограничивает величину идеального остатка до - Vr/4. Несмотря на то, что данный пример показан только для уровня 2б, такой подход работает на любом уровне. К примеру, циклический АЦП с одним дополнительным компаратором. Главное преимущество этой технологии - уменьшение величины идеального остатка до 1/2 LSB на отдельном уровне, сокращение необходимого размаха сигнала на выходе при межкаскадном усилении, уменьшение чувствительности к ошибкам усиления так же, как и на рис. 3а. Важность этого преимущества, однако, уменьшается из-за присутствия нелинейности ADSC, которая увеличивает максимальную величину остатка около затронутых значений. Кроме того, функциональное тестирование АЦП все еще не полностью тестирует логику коррекции, потому что неисправленные на выходе коды не показывают какое увеличение или изменение они претерпели по сравнению с входным сигналом. Поэтому, основные недостатки этого метода заключаются в требовании дополнительных компараторов и в проблематичности проверки корректирующей логики. Чтобы преодолеть эти проблемы вместо большого количества компараторов в ADSC, их используется на один меньше.

Поскольку диапазон исправления на рис. 3б ±1/2LSB на 2-б уровне и потому, что главный уровень сигнала 1/2LSB на уровне ниже полного масштаба рис. 3б, показывает также, что компаратор не обязателен на всех уровнях, кроме последнего. Его удаление вызывает ошибку, которую можно исправить при выходном полномасштабном сигнале ADSC. Рисунок 5 показывает график идеального остатка от сигнала на уровне 2-б. (Смещение компаратора здесь принято равным нулю.) Без главного компаратора цифровой сигнал на выходе никогда не достигнет значения 11 и остаток будет повышаться и увеличится больше, чем до 1/4. Поскольку остаток в правом конце (рис. 5) имеет ту же величину, что и остаток в левой части (рис. 3б и рис. 5), удаление главного компаратора не увеличивает величину максимального остатка. Для получения кода 11 из этого этапа логика исправления ошибок постепенно увеличивает результат этого этапа. Кроме того, для получения кода 00 на выходе с этого уровня после исправления коррекционная логика ничего не должна делать, так как нет операции вычитания. Таким образом, возможность корректирующей логики выполнять оба типа действия (сложение и отсутствие каких-либо изменений), может быть проверена просто тестированием всего АЦП на присутствие всех его возможных комбинаций на выходе. Это значительно упрощает тестирование корректирующей логики.

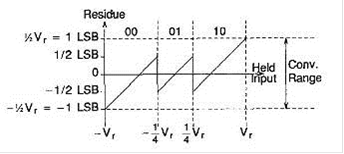
Рисунок 5 - Идеальный остаток сигнала без главного компаратора

Кроме того, после удаления главного компаратора диапазон коррекции останется ±1/2LSB на уровне 2-б, потому что находящиеся уровни сигнала могут быть сдвинуты выше до получившегося остатка и превышать уровень преобразования следующего этапа. Поэтому в данном примере необходимы только два компаратора на каждом этапе, кроме последнего. На последнем этапе все еще требуется 3 компаратора для исправления выходного сигнала. В целом, если n - число выходных битов на этап, то на каждом уровне требуется компараторов, кроме последнего, на котором нужен компаратор. В результате разрешение каждого этапа кроме последнего равно бит. Если n = 2, как в нашем примере, разрешение каждого уровня будет 1,5 бита и архитектура идентична предложенной Юсуфом (17 в списке литературы), потому что 1 битный ADSC с добавленным компаратором тоже самое что 2 битный ADSC без компаратора. Уменьшение количества компараторов уменьшает общую площадь на кристалле и рассеиваемую мощность, а так же емкостную нагрузку на каждую схему выборки/хранения SHA. Это также сокращает требуемое количество уровней в ЦАП, что важно, так как это способствует увеличению скорости и уменьшает его чувствительность к емкостной ошибке.

Интересное из раздела

Функционально-структурный анализ системы автоматического управления (регулирования) технического объекта
Работа любого технологического объекта характеризуется различными параметрами, которые изменяются в зависимости от работы машины и воздействия внешних факто ...

Исследование и расчет цепей синусоидального тока
Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону: , где - максимальное значение или амплитуда ...

Исследование аналого-цифрового и цифрового преобразователей
Аналого-цифровые преобразователи предназначены для преобразования непрерывных (аналоговых) сигналов в дискретные (цифровые), которые могут использоваться в ...